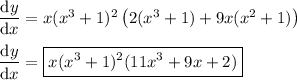Question

Tính đạo hàm y= ( x^2+1)(x^3+1)^3

Answer 1

Use the product, power, and chain rules.

`y = (x^2 + 1) (x^3 + 1)^3`

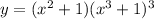
Differentiate both sides:

`(\mathrm dy)/(\mathrm dx) = (\mathrm d\left((x^2 + 1) (x^3 + 1)^3\right))/(\mathrm dx)`

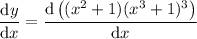
Product rule:

`(\mathrm dy)/(\mathrm dx) = (\mathrm d(x^2 + 1))/(\mathrm dx)(x^3+1)^3 + (x^2+1)(\mathrm d(x^3 + 1)^3)/(\mathrm dx)`

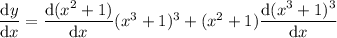
Power rule for the first derivative, power and chain rules for the second one:

`(\mathrm dy)/(\mathrm dx) = 2x(x^3+1)^3 + 3(x^2+1)(x^3+1)^2(\mathrm d(x^3 + 1))/(\mathrm dx)`

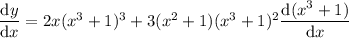
One last applicaton of power rule:

`(\mathrm dy)/(\mathrm dx) = 2x(x^3+1)^3 + 9x^2(x^2+1)(x^3+1)^2`

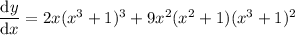
You could stop here, or continue and simplify the result by factorizing:

`(\mathrm dy)/(\mathrm dx) = x(x^3+1)^2 \left(2(x^3+1) + 9x(x^2+1)\right) \\\\ (\mathrm dy)/(\mathrm dx) = \boxed{x(x^3+1)^2 (11x^3+9x+2)}`