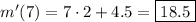Using the product rule, we have
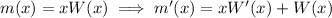
so that
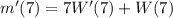
The equation of the tangent line to W(x) at x = 7 has all the information we need to determine m' (7).
When x = 7, the tangent line intersects with the graph of W(x), and
y = 4.5 + 2 (7 - 7) ==> y = 4.5
means that this intersection occurs at the point (7, 4.5), and this in turn means W (7) = 4.5.
The slope of this tangent line is 2, so W' (7) = 2.
Then