Question

I've tried this multiple times and cant seem to get the right answer could someone help solve this?

Answer 1

Recall the double angle identity for cosines

• 
  `{\boxed{\bf{2\cos^(2)(\theta)=1+\cos (2\theta)}}}`

Using this the integral becomes :

`{:\implies \quad \displaystyle \sf (1)/(2)\int_{\tiny (\pi)/(3)}^{\tiny (\pi)/(2)}\{3\cos (\theta)\}^(2)d\theta}`

`{:\implies \quad \displaystyle \sf (1)/(2)\int_{\tiny (\pi)/(3)}^{\tiny (\pi)/(2)}9\cos^(2)(\theta)d\theta}`

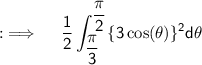
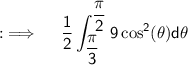
As we can take constant out of the integrand so we have

`{:\implies \quad \displaystyle \sf (9)/(2)\int_{\tiny (\pi)/(3)}^{\tiny (\pi)/(2)}\cos^(2)(\theta)d\theta}`

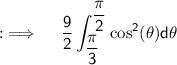
Using the double angle identity for cosines ;

`{:\implies \quad \displaystyle \sf (9)/(2)\int_{\tiny (\pi)/(3)}^{\tiny (\pi)/(2)}\bigg\{(1+\cos (2\theta))/(2)\bigg\}d\theta}`

`{:\implies \quad \displaystyle \sf (9)/(4)\int_{\tiny (\pi)/(3)}^{\tiny (\pi)/(2)}\{1+\cos (2\theta)\}d\theta}`

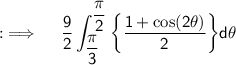
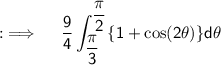
Now , as integrals follow distributive property, so we now have

`{:\implies \quad \displaystyle \sf (9)/(4)\bigg(\int_{\tiny (\pi)/(3)}^{\tiny (\pi)/(2)}d\theta+\int_{\tiny (\pi)/(3)}^{\tiny (\pi)/(2)}\cos (2\theta)d\theta \bigg)}`

`{:\implies \quad \displaystyle \sf (9)/(4)\bigg\{\bigg(\theta +(\sin (2\theta))/(2)\bigg) \bigg|_{\tiny (\pi)/(3)}^{\tiny (\pi)/(2)}\bigg\}}`

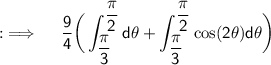
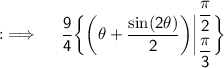
`{:\implies \quad \displaystyle \sf (9)/(4)\bigg[(\pi)/(2)-(\pi)/(3)+(1)/(2)\bigg\{\sin (\pi)-\sin \left((2\pi)/(3)\right)\bigg\}\bigg]}`

`{:\implies \quad \displaystyle \sf (9)/(4)\bigg\{(3\pi -2\pi)/(6)+(1)/(2)\bigg(-(√(3))/(2)\bigg)\bigg\}}`

`{:\implies \quad \displaystyle \sf (9)/(4)\bigg((\pi)/(6)-(√(3))/(4)\bigg)}`

`{:\implies \quad \displaystyle \sf (9)/(4)\bigg((2\pi -3√(3))/(12)\bigg)}`

`{:\implies \quad \displaystyle \sf (3(2\pi -3√(3)))/(4* 4)}`

`{:\implies \quad \displaystyle \sf (6\pi -9√(3))/(16)}`

`{:\implies \quad \displaystyle \bf \therefore \quad \underline{\underline{\int_{\tiny (\pi)/(3)}^{\tiny (\pi)/(2)}\{3\cos (\theta)\}^(2)d\theta =(6\pi -9√(3))/(16)}}}`

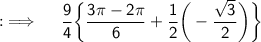
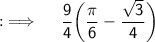
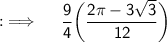
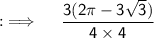
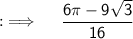
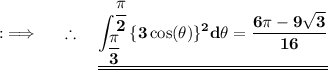
Used Concepts :-

• 
  `{\boxed{\displaystyle \bf \int dx=x+C}}`

• 
  `{\boxed{\displaystyle \bf \int \cos (nx)dx=(\sin (nx))/(n)+C}}`

Answer 2

`(6\pi -9√(3) )/(16)`

Explanation:

You need to rewrite
`\cos^2 \theta` using cos double angle identity:

`\cos 2\theta= \cos^2\theta-\sin^2\theta`

`\implies \cos 2\theta= \cos^2\theta-(1-\cos^2\theta)`

`\implies \cos 2\theta=2 \cos^2\theta-1`

`\implies \cos^2\theta=\frac12(\cos 2\theta+1)`

Then substitute this into the integration.

Please see the attachment for the full integration (it was clearer for me to type this in MS word than use the equation editor here)