Question

Find the slope-intercept form of the equation of the line with the given properties.Horizontal; containing the point (-\frac{5}{6},2)(−65​,2)

Answer 1

Answer: y=2

Explanation:

Slope-intercept form is y=mx+b, where m is slope and b is y-intercept. To find slope, we use the formula
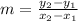`m=(y_2-y_1)/(x_2-x_1)`. We use the points given to plug into the formula.

`m=(2-2)/(-65-(-(5)/(6)) ) =(0)/(-(385)/(6) ) =0`

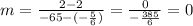
Now that we know the slope is 0, we know that the y-intercept is also 2.

Actually, we did not have to do this because we know that the line is horizontal based on the properties. So we know the equation should be y=b. Notice the y-coordinate is 2 for both points.

Therefore, the equation would be y=2.