Question

A car traveling at 27 m/s runs out of gas while traveling up a 8.0 ∘ slope. How far will it coast before starting to roll back down?

Answer 1

Approximately
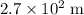`2.7 * 10^(2)\; \rm m` along the slope, assuming that no energy was lost to friction.

Step-by-step explanation:

Let
`v` denote the initial velocity of this vehicle. Let
`m` denote the mass of this vehicle. The kinetic energy (KE) of this vehicle would have initially been:

`\displaystyle (1)/(2)\, m \cdot v^(2)`.

The gain in the gravitational potential energy (GPE) of this vehicle is proportional to the increase in its height.

Let
`g` denote the gravitational field strength.
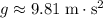`g \approx 9.81\; \rm m \cdot s^(2)` on the earth. If the increase in the height of this vehicle is
`h`, this vehicle would have gained GPE:

`m \cdot g \cdot h`.

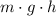Hence, the height of this vehicle is maximal when the GPE of this vehicle is maximized.

Since the vehicle went out of fuel, all its GPE would have been converted from KE. Assuming that no energy was converted to friction. The GPE of this vehicle would be maximal when the entirety of the KE was converted to GPE.

Hence, the maximal GPE of this vehicle would be equal to its initial KE:

`\displaystyle m \cdot g \cdot h = (1)/(2)\, m \cdot v^(2)`.

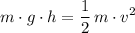The maximum height of this vehicle would be:

`\begin{aligned} h &= ((1/2) \, m \cdot v^(2))/(m \cdot g)\\ &= (v^(2))/(2\, g)\end{aligned}`.

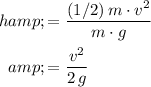Given that
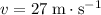`v = 27\; \rm m\cdot s^(-1)`, the maximum height of this vehicle would be:

`\begin{aligned} & (v^(2))/(2\, g) \\ =\; & ((27\; \rm m\cdot s^(-1))^(2))/(2 * 9.81\; \rm m\cdot s^(-2)) \\ \approx \; &37.2\; \rm m\cdot s^(-1)\end{aligned}`.

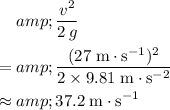Refer to the diagram attached. The distance that this vehicle traveled along the slope would be approximately:

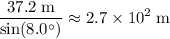`\begin{aligned}(37.2\; \rm m)/(\sin(8.0^(\circ))) \approx 2.7 * 10^(2)\; \rm m\end{aligned}`.