Answer:

Explanation:
Hi there!
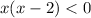
Set x(x-2) equal to 0:
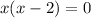
Solve for x by using the zero product property:
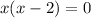
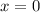 and
and
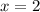
Now, we know that for the inequality
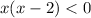 , one of the following must be true:
, one of the following must be true:
1)

2)
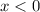 or
or
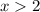
To find out which one it is, 1) or 2), we can substitute a value into
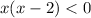 to see if the inequality is true.
to see if the inequality is true.
For example, 1 takes place in between 0 and 2. If 1 satisfies
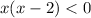 , then
, then
 must be true. If it does not, then
must be true. If it does not, then
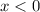 or
or
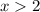 must be true:
must be true:
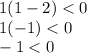
This inequality is true. Thus,
 .
.
I hope this helps!