Answer:
 .
.
Explanation:
Apply polynomial long division to divide
 by the know factor,
by the know factor,
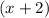 .
.
Fill in the omitted terms:
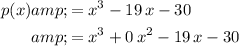 .
.
The leading term of the dividend is currently
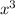 . On the other hand, the leading term of the divisor,
. On the other hand, the leading term of the divisor,
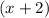 , is
, is
 .
.
Hence, the next term of the quotient would be
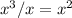 .
.
![\begin{aligned}p(x) &= \cdots \\ &= x^(3) + 0\, x^(2) - 19\, x - 30 \\ &= x^(3) + 0\, x^(2) - 19\, x - 30 \\ &\quad - x^(2) \, (x + 2) + [x^(2) \, (x + 2)] \\ &= x^(3) + 0\, x^(2) - 19\, x - 30 \\ &\quad -x^(3) - 2\, x^(2) + [x^(2)\, (x + 2)] \\ &= -2\, x^(2) - 19\, x - 30 \\ &\quad + [x^(2) \, (x + 2)]\end{aligned}](https://img.qammunity.org/2022/formulas/mathematics/high-school/2qc7rxy8afp2dyt55vh1rclndej5is2rdt.png) .
.
The dividend is now
 , with
, with
 being the new leading term. The leading term of the divisor
being the new leading term. The leading term of the divisor
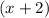 is still
is still
 .
.
The next term of the quotient would be
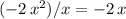 .
.
![\begin{aligned}p(x) &= \cdots \\ &= -2\, x^(2) - 19\, x - 30 \\ &\quad + [x^(2) \, (x + 2)] \\ &=-2\, x^(2) - 19\, x - 30 \\ &\quad - (-2\,x ) \, (x + 2) + [(-2\, x) \, (x + 2)] + [x^(2) \, (x + 2)] \\ &= -2\, x^(2) - 19\, x - 30 \\ &\quad - (-2\, x^(2) - 4\, x) + [(x^(2) - 2\, x)\, (x + 2)] \\ &= -15\, x - 30 \\ &\quad + [(x^(2) - 2\, x)\, (x + 2)]\end{aligned}](https://img.qammunity.org/2022/formulas/mathematics/high-school/kupdf79dsphcezrfrp28ny3k8nj13ahrhu.png) .
.
The dividend is now
 , with
, with
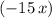 as the new leading term.
as the new leading term.
The next term of the quotient would be
 .
.
![\begin{aligned}p(x) &= \cdots \\ &= -15\, x - 30 \\ &\quad + [(x^(2) - 2\, x)\, (x + 2)] \\ &=-15\, x - 30 \\ &\quad -(-15)\, (x + 2) + [(-15)\, (x + 2)] + [(x^(2) - 2\, x)\, (x + 2)] \\ &= -15\, x - 30 \\ &\quad -(-15\, x - 30) + [(x^(2) - 2\, x - 15)\, (x + 2)] \\ &= (x^(2) - 2\, x - 15)\, (x + 2)\end{aligned}](https://img.qammunity.org/2022/formulas/mathematics/high-school/7sihh7eiv5kqwgsxtjz4g8barxq0kh2apu.png) .
.
In other words:
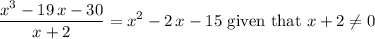 .
.
The next step is to factorize the quadratic polynomial
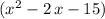 .
.
Apply the quadratic formula to find the two roots of
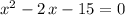 :
:
 .
.
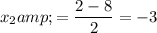 .
.
By the factor theorem, the two factors of
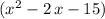 would be
would be
 and
and
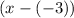 . That is:
. That is:
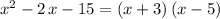 .
.
Therefore:
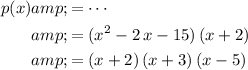 .
.