Question

X^2 - 2x + 1
x^2 - 2x - 1
x^2 + 2x + 1
In the denominator

Answer 1

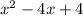`x^(2) -4x+4` in the numerator

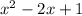`x^(2) -2x+1` in the denominator

Explanation:

First fraction simplifies to:

`(x^(2)+x-6)/(x^(2)-6x+5)\\(x^(2)-2x+3x-6)/(x^(2)-x-5x+5)\\(x(x-2)+3(x-2))/(x(x-1)+5(x-1))\\((x+3)(x-2))/((x-1)(x+5))\\`

Dividing my a fraction is the same as multiplying by the reciprocal, so the second fraction simplifies to:

`(x^(2)-7x+10)/(x^(2)+2x-3)\\(x^(2)-2x+5x-10)/(x^(2)-x+3x-3)\\(x(x-2)+5(x-2))/(x(x-1)+3(x-1))\\((x+5)(x-2))/((x-1)(x+3))\\`

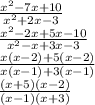
So the equation becomes:

`((x+3)(x-2))/((x+5)(x-1)) * ((x+5)(x-2))/((x-1)(x+3))\\`

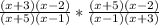
The (x+3) and (x+5) terms cancel out, so what your left with is

`((x-2)^(2))/((x-1)^(2))`

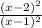
Expanding this term you get the answer:

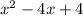`x^(2) -4x+4` in the numerator

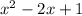`x^(2) -2x+1` in the denominator