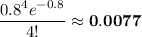1. The table shows the probability of selling x houses in one day. So
P(X = 4) = 0.0551
2. Consult the table.
P(X = 0) = 0.2019
3. Add up the probabilities of selling at least 5 houses:
P(X = 5) + P(X = 6) + P(X = 7) + P(X = 8) + P(X = 9) + …
By nature of the Poisson distribution, the probability of selling more than 9 houses is so close to 0 it may as well be. So we stop where the table does.
P(X = 5) + P(X = 6) + P(X = 7) + P(X = 8) + P(X = 9)
= 0.0176 + 0.0047 + 0.0011 + 0.0002 + 0.0000
= 0.0236
4. As alluded in the previous answer,
P(X ≥ 10) ≈ 0
5. This requires some knowledge about the Poisson distribution. If an average of λ houses/day is sold, then the probability of selling x houses on a given day is

If an average of 1.6 houses are sold each day, then in two days the average sold is
(1.6 houses) / (2 days) = 0.8 houses/day
and this follows another Poisson distribution with mean 0.8. Then the probability of selling 4 houses in two days is