Question

The equation −16x2 + 10x + 15 = 0 represents the height, in feet, of a flotation device above the water after x seconds. The linear term represents the initial velocity. The constant term represents the initial height.

a. If the initial velocity is 0, when should the flotation device land in the water?
b. If the initial height is 0, when does the flotation device land in the wate

Answer 1

a) 0.968 s (nearest thousandth)

b) 0.625 s

Explanation:

Give equation:
`-16x^2 + 10x + 15 = 0`

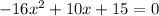
If the linear term represents the initial velocity,
then the initial velocity in the original equation = 10 ft/s

If the constant term represents the initial height,
then the initial height in the original equation = 15 ft

a) If the initial velocity is 0

`\implies -16x^2 + 15 = 0`

`\implies x^2 = (15)/(16)`

`\implies x = \pm(√(15))/(4)`

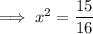
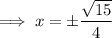
As time is positive,

`\implies x =(√(15))/(4)=0.9682458366...`

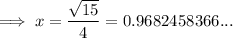
The flotation device will hit the water after 0.968 s (nearest thousandth)

b) If the initial height is 0:

`\implies -16x^2 + 10x = 0`

`\implies -2x(8x-5) = 0`

`\implies -2x=0\implies x=0`

`\implies 8x-5=0 \implies x=\frac58`

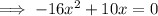
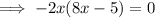
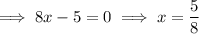
Therefore, the flotation device lands in the water after 5/8 seconds = 0.625 s