Question

Calculus again!

A yo-yo is moving up and down a string so that its velocity at time t is given by v(t) = 4cos(t) for time t ≥ 0. The initial position of the yo-yo at time t = 0 is x = 4. Find the displacement and distance from time t = 0 to time t = π.
I know that the displacement would be calculated by
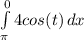
`\int\limits^0_\pi {4cos(t)} \, dx` and the displacement would be calculated by
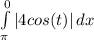
`\int\limits^0_\pi \, dx`, but would both be 0? Thank you!

Answer 1

Not. Both are diferent.

The displacement from time t = 0 to time t = π is given by:

`{\displaystyle s = \int _0^(\pi )4\cos\left(t\right)\:dt}`

`{\displaystyle s = 4\left[\sin \left(t\right)\right]^(\pi )_0}`

`s = 4[0 - 0 ]`

`s = 0`

The distance from time t = 0 to time t = π is:

`4\cos\left(t\right)`

`{\displaystyle d = \int _0^{(\pi )/(2)}4\cos \left(t\right)dt+\int _{(\pi )/(2)}^(\pi )-4\cos \left(t\right)dt}`

`d = 4\left[\sin \left(t\right)\right]^{(\pi)/(2)}_0 - 4\left[\sin \left(t\right)\right]^(\pi)_{(\pi)/(2)}`

`d = 4 + 4`

`d = 8`