Question

`f(x) = x {}^(2) + 12x + 36`

Determine the value of f^-1 (225) in this situation.
A. 21 days

B. 9 days

C. 6 days

D. 15 days​

Answer 1

B

Explanation:

We are given the function:

`\displaystyle f(x) = x^2 + 12x + 36`

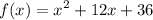
And we want to determine the value of:

`\displaystyle f^(-1)(225)`

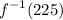
Let this value equal a. In other words:

`\displaystyle f^(-1)(225) = a`

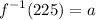
Then by the definition of inverse functions:

`\displaystyle \text{If } f^(-1)(225) = a\text{, then } f(a) = 225`

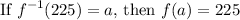
Hence:

`\displaystyle f(a) =225 = (a)^2 + 12(a) + 36`

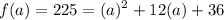
Solve for a:

`\displaystyle \begin{aligned} 225 &= a^2 + 12a + 36 \\ \\ a^2 + 12a -189 &= 0 \\ \\ (a + 21)(a-9) &= 0\end{aligned}`

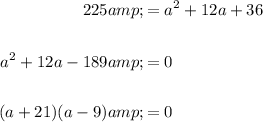
By the Zero Product Property:

`\displaystyle a + 21 = 0 \text{ or } a - 9 = 0`

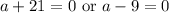
Hence:

`\displaystyle a = -21 \text{ or } a = 9`

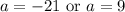
Thus, f(9) = 225. Consequently, f⁻¹(225) = 9.

In conclusion, our answer is B.