Question

Calculate the distance between the points J= (2, -3) and Q=(9,-9) in the coordinate plane.

Round your answer to the nearest hundredth.

Answer 1

9.22

Explanation:

First, let's establish the distance formula! The distance formula is
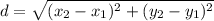`d = \sqrt{(x_(2) - x_(1))^2 + (y_(2) - y_(1))^2`. Now, let's input our variables into the formula.

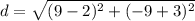`d = √((9-2)^2 + (-9 + 3)^2)` (Also, we changed the minus sign to a plus sign because we have a negative number and we know that a negative minus a negative is a positive!) Now we can start to solve the equations!

1st. We need to solve inside the parenthesis of both the x parenthesis and the y parenthesis.

`d = √((7)^2 + (-6)^2)`

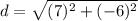
2nd. We should square the inside of both of the parenthesis!

`d = \sqrt{49 + 36` (Remeber that when you square a negative you get a positive)

3rd. Then, we can add 49 and 36!

`d = √(85)`

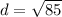
4th. Lastly, we are going to find the square root of 85.

d ≈ 9.22 (Remember that "≈" means the round solution, in this case we are rounding to the nearest 100th!)

Hope this Helps! :)

Have any questions? Ask below in the comments and I will try my best to answer.

-SGO