Answer: Choice B
===================================================
Step-by-step explanation:
Let's look at choice A
The left hand side simplifies as follows
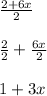
This means the equation
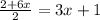 is the same as
is the same as
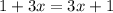 . Notice how the left and right sides are identical expressions. They both involve 3x and a 1. This means this equation has infinitely many solutions. We can rule out choice A.
. Notice how the left and right sides are identical expressions. They both involve 3x and a 1. This means this equation has infinitely many solutions. We can rule out choice A.
------------------------------
I'll skip choice B and come back
Let's move onto choice C.
The given equation
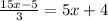 transforms into
transforms into
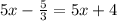 through similar steps as choice A shows.
through similar steps as choice A shows.
If we were to subtract 5x from both sides, all of the x terms go away on both sides. We'd be left with the equation
 which is always false, which means that the original equation is always false.
which is always false, which means that the original equation is always false.
Therefore, the equation of choice C has no solutions. We consider this equation inconsistent. We rule out choice C because of all this.
------------------------------
Choice D is pretty much the same as choice A even down to the conclusion of getting infinitely many solutions. The left hand side simplifies fully into the right hand side. The two sides are identical; hence, we have an identity. An identity is true for all allowed x values in the domain.
In other words, whatever x value you pick it will make the equation true. So we can rule this out because we want one solution only.
------------------------------
Only choice B is left. You'll notice that after simplifying the left hand side, the x term on the left side doesn't turn into 2x. So there's no way to get the options of "infinitely many solutions" or "no solutions". Those two cases only happen when we have the same x terms on both sides.
Put another way, the two slopes of each side are different which produces nonparallel lines that intersect at exactly one location. This intersection location is the solution. Specifically, the x coordinate of the (x,y) location is the solution.