Question

Find the value of k such that x-2 is a factor of 3x³-kx²+5x+k​

Answer 1

`\displaystyle k = (34)/(3)`

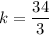
Explanation:

We are given the polynomial:

`\displaystyle P(x) = 3x^3 - kx^2 + 5x + k`

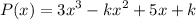
And we want to determine the value of k such that (x - 2) is a factor of the polynomial.

Recall that the Factor Theorem states that a binomial (x - a) is a factor of a polynomial P(x) if and only if P(a) = 0.

Our binomial factor is (x - 2). Thus, a = 2.

Hence, by the Factor Theorem, P(2) must equal zero.

Find P(2):

`\displaystyle \begin{aligned} P(2) &= 3(2)^3 - k(2)^2 + 5(2) + k \\ \\ &= 3(8) - 4k + 10 + k \\ \\ &= 34 - 3k \end{aligned}`

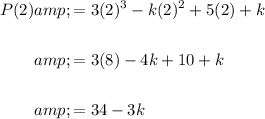
This must equal zero. Hence:

`\displaystyle \begin{aligned} 34 - 3k &= 0 \\ \\ -3k &= -34 \\ \\ k = (34)/(3) \end{aligned}`

In conclusion, k = 34/3.