Answer:
Use Distance Formula
Explanation:
You can find the distance between two points by using the distance formula which by definition is
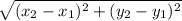
For example take question 3. Plug your point values in to find the distance
Point 1 is (-1, 8)
Point 2 is (-3, -2)
You equation would look like:
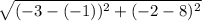
This simplifies to
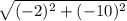
=
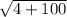
=
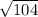
=
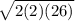
=
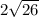
That is the distance between the points (-1, 8) and (-3, -2)