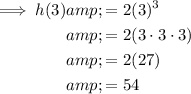Answer:
a) 4
b) 10
c) 54
Explanation:
Given functions:
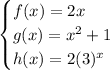
Part (a)
To find f(2), substitute x = 2 into function f(x) and solve:
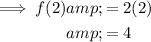
Part (b)
To find g(-3), substitute x = -3 into function g(x) and solve:
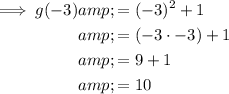
Part (c)
To find h(3), substitute x = 3 into function h(x) and solve: