Question

How do I solve this limits problem?

Please don't just give me the answer; I'd like to know how to actually do this. Thanks in advance.

Answer 1

Each piece of this function is continuous on its respective domain (because all polynomials are continuous functions), meaning

• 2 - x exists for all x < -1

• x exists for all -1 ≤ x < 1

• (x - 1)² exists for all x ≥ 1

So this really just leaves the points where the pieces are split up, i.e. x = -1 and x = 1. At both of these points, the two-sided limit exists as long as the one-side limits from both sides exist and are equal to one another.

At x = -1, as I said in my comment, you have

`\displaystyle \lim_(x\to-1^-)f(x) = \lim_(x\to-1)(2-x) = 2-(-1) = 3`

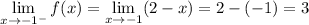
while

`\displaystyle \lim_(x\to-1^+)f(x) = \lim_(x\to-1)x = -1`

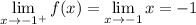
But -1 ≠ 3, so the two-sided limit

`\displaystyle\lim_(x\to-1)f(x)`

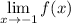
does not exist. So a = -1 is one of the points you would list.

At x = 1, we have

`\displaystyle \lim_(x\to1^-)f(x) = \lim_(x\to1)x = 1`

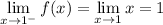
while

`\displaystyle \lim_(x\to1^+)f(x) = \lim_(x\to1)(x-1)^2 = (1-1)^2 = 0`

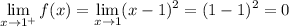
and again the one-sided limits don't match, so this two-sided limit also does not exist, making a = 1 the other answer.