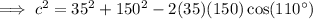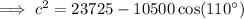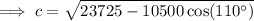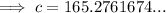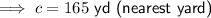Question

NO LINKS!!! Part 7: Please help me with this problem​

Answer 1

Apply law of cosines

`\\ \rm\longmapsto c^2=a^2+b^2-2abcos\gamma`

`\\ \rm\longmapsto c^2=150^2+35^2-2(150)(35)cos110`

`\\ \rm\longmapsto c^2=22500+1225-10500(-0.34)`

`\\ \rm\longmapsto c^2=23725+3570`

`\\ \rm\longmapsto c^2=27295`

`\\ \rm\longmapsto c=165.2yd`

Answer 2

165 yd (nearest yard)

Explanation:

To calculate the distance from the ball to the center of the green, we need to use the cosine rule:

`c^2=a^2+b^2-2ab \cos (C)`

where:

• C is the angle
• a and b are the sides adjacent to the angle C
• c is the side opposite the angle C

Therefore, for this triangle:

• a = 35 yd
• b = 150 yd
• C = 110°

Substituting these values into the cosine rule formula:

`\implies c^2=35^2+150^2-2(35)(150) \cos (110\textdegree)`

`\implies c^2=23725-10500\cos(110\textdegree)`

`\implies c=√(23725-10500 \cos(110\textdegree))`

`\implies c=165.2761674...`

`\implies c = 165 \textsf{ yd (nearest yard)}`