Answer: Lines
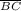 and
and
 are different lengths.
are different lengths.
Step-by-step explanation:
The distance formula is
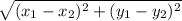 , and you can use this formula to solve for the lengths of both lines
, and you can use this formula to solve for the lengths of both lines
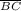 and
and
 .
.
For line
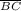 , let
, let
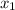 = the x at point B, or 1, and let
= the x at point B, or 1, and let
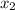 = the x at point C, or 2.
= the x at point C, or 2.
Now, let
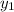 = the y at point B, or 4, and let
= the y at point B, or 4, and let
 = the y at point C, or -1.
= the y at point C, or -1.
Now, solve the formula to find the length
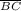 =
=
 .
.
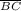 =
=

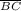 =
=
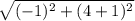
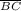 =
=
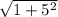
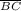 =
=
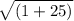
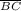 =
=
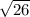
Now, for line
 , let
, let
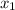 = the x at point E, or -4, and let
= the x at point E, or -4, and let
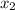 = the x at point F, or -1.
= the x at point F, or -1.
Let
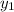 = the y at point E, or -3, and let
= the y at point E, or -3, and let
 = the y at point F, or 1.
= the y at point F, or 1.
Now, solve the formula to find the length
 =
=
 .
.
 =
=
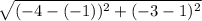
 =
=
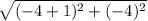
 =
=
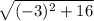
 =
=

 =
=

 = 5
= 5
Now, look back at
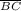 . The two lines have different lengths, so you have now justified the fact that they are not the same.
. The two lines have different lengths, so you have now justified the fact that they are not the same.
Questions 13 and 14 would be solved in much the same way- but please let me know if you want me to show the work for those as well!