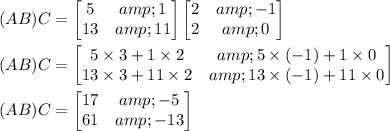Given
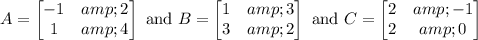
we have
(1)

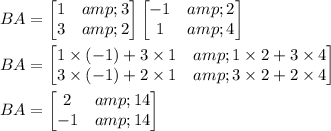
So AB ≠ BA. This is generally true for arbitrary matrices A and B, since matrix multplication is not commutative.
(2)

so we have 2BC = 2B•2C = 4BC if and only if BC is the zero matrix.
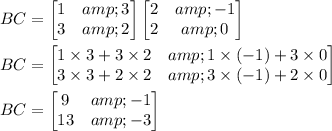
So 2BC ≠ 2B•2C.
(3) Yes, (AB)C = A(BC) because matrix multplication is associative. You don't need to compute this, but just to confirm this result: