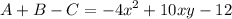Answer:
I)
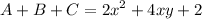
II)
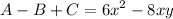
III)
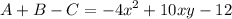
Explanation:
We are given the three equations:
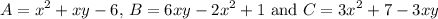
I)
We want to find:
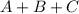
Substitute:
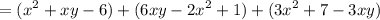
Rewrite:
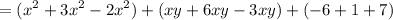
And combine like terms. Hence:
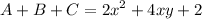
II)
We want to find:
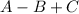
Likewise, substitute:
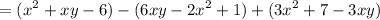
Distribute:
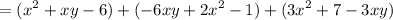
Rewrite:
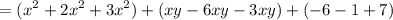
And combine like terms. Hence:
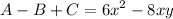
III)
We want to find:
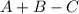
Substitute:
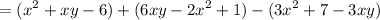
Distribute:
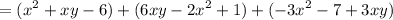
Rewrite:
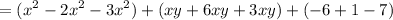
And combine like terms. Hence: