Answer:
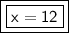
Explanation:
We are asked to solve for x. We are given a triangle and all 3 angles are labeled. We know that the sum of the angles in a triangle must be 180 degrees. Therefore, the given angles: 81, 57, and (2x+18) must add to 180. We can set up an equation.

Now we can solve for x. Begin by combing like terms on the left side of the equation. All the constants (terms without a variable) can be added.
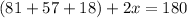
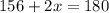
We will solve for x by isolating it. 156 is being added to 2x. The inverse operation of addition is subtraction. Subtract 156 from both sides of the equation.
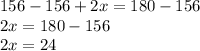
x is being multiplied by 2. The inverse operation of multiplication is division. Divide both sides by 2.
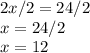
In this triangle, x is equal to 12.