Answer:
The slope of line perpendicular to the line segment that has a slope of
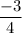 is
is

Explanation:
Given,
The line segment has a slope of
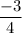 .
.
To find:
The slope of the line that is perpendicular to the given line segment.
Now,
Let suppose a line
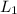 has a slope
has a slope
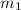 and line
and line
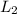 has a slope
has a slope
 .
.
Condition for perpendicularity:
If the product of the slopes of these lines equals -1, then the lines are perpendicular to each other.
Therefore, apply the above condition to our question.
So,
