Answer:
55.9 feet
Explanation:
Basically you can just plug in what they give you
givens:
V=60 ft/sec
a= 32.2 ft/sec^2
function to find velocity:
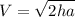
if you plug everything in:
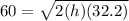
you can just put that equation into a website and ask it to solve for h which would give you your answer
but, if you want the work,
FIRST square both sides of the equation to get rid of the square root symbol on the left so,
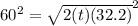
which cancels out to
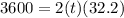
NEXT: divide both sides by 32.2 to get 2t by its self so,
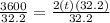
which should get you to
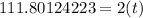
LAST: divide both sides by 2 to get t by itself so
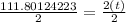
and you should end up with
55.900621 = t
which rounded would be an answer of
t= 55.9 feet