Question

Evaluate the limit of sequence at infinity.


`\displaystyle \large{ \lim_(n \to \infty ) \frac{ \sqrt{4 {n}^(2) + 3n } }{6n} }`
Please show your work too. Thanks!​

Answer 1

`\displaystyle ( 1 )/(3)`

Explanation:

we would like to compute the following limit:

`\displaystyle \lim_(n \to \infty ) \frac{ \sqrt{4 {n}^(2) + 3n } }{6n}`

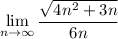
if we compute the limit from numerator to denominator directly,we'd end up with

`( \infty )/( \infty )`

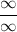
which is an indeterminate form so we must do it in a different way. well to compute this limit,we can consider factoring method . notice that we can factor the numerator and that yields

`\displaystyle \lim_(n \to \infty ) \frac{ \sqrt{ {n}^(2) ( 4 {}^{} + (3)/(n) )} }{6n}`

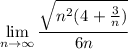
remember that ,

• 
  `√(ab) \implies √(a) √(b)`

thus we acquire:

`\displaystyle \lim_(n \to \infty ) \frac{ {n} \sqrt{ ( 4 {}^{} + (3)/(n) )} }{6n}`

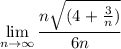
reduce fraction:

`\displaystyle \lim_(n \to \infty ) \frac{ {} \sqrt{ 4 {}^{} + (3)/(n) } }{6}`

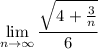
as n approaches to ∞ ,3/n approaches to 0 which yields:

`\displaystyle \frac{ \sqrt{ 4 {}^{} } }{6}`

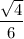
simplify square root:

`\displaystyle ( 2 )/(6)`

reduce fraction:

`\displaystyle ( 1 )/(3)`

hence,

`\displaystyle \lim_(n \to \infty ) \frac{ \sqrt{4 {n}^(2) + 3n } }{6n} = \boxed{ (1)/(3) }`

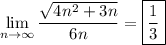
and we're done!