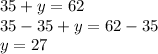Question

The sum of two numbers is 62, and their difference is 8. What are the
numbers?

Answer 1

Answer: 35 and 27

Explanation:

We can solve this by using a system of equations

x will be the first number while y will be the second

`x+y=62`

This equation means the two numbers will add to get 62

`x-y=8`

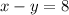
This equation means when subtracted the two numbers will have the difference of 8.

Now I will solve by elimination

`x+y=62\\\\+x-y=8\\2x=70`

When adding the two equations why was eliminated so now we can find the value of x

`2x=70\\(2x)/(2) =(70)/(2) \\x=35`

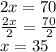
Now sub in x into one of the original equations to find the value of y

`35+y=62\\35-35+y=62-35\\y=27`