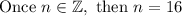Answer:
See below
Explanation:
We have the series
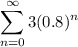
(a) To show that the sum of first
 terms is
terms is
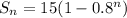
Consider that the this sum is given as
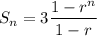
In this case, the ratio is 0.8, thus,
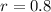
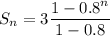
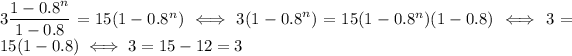
Therefore,
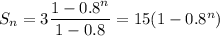

(b) Calculate the smallest integer value of
 such that
such that
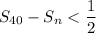
Once
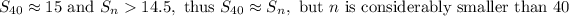
I am considering
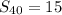 , so
, so