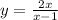Answer:
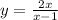
Explanation:
find the inverse of the function
To find the inverse function, swap x and y, and solve the resulting equation for x.
If the initial function is not one-to-one, then there will be more than one inverse.
So, swap the variables
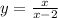
becomes
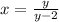
Now, solve the equation
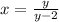
for y.