Explanation:
46. The midsegment Theorem states that a line segment connecting the midpoints of the legs of the trapezoid is parallel to the bases, and equal to half their sum.
Using this info,
We already know EF=11 so
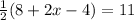
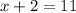
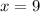
53. Apply Midpoint Formula
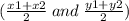
Let find the midpoint of each side
KL (+2a/2, +2a/2), LM(-2a/2, 2a/2) MN(-2a/2, -2a/2) NK(2a/2, -2a/2)
So the midpoint of each side is
KL=(a,a)
LM= (-a,a)
MN=(-a,-a)
NK=(a,-a).
The slopes of these line is y2-y1/x2-x1
KL=2a/-2a=-a
LM=-2a/-2a=a
MN=-2a/2a=-a
NK=-2a/-2a=a
Let find the length of all sides. Since each coordinate has a form of 0 in it, we would just consider the finite value, 2a.
Distance of all sides are 2a.
Consider the midpoint, notice how each midpoint can be obtained by a rotation of 90-180-270 or 360 degrees about the origin of one of the midpoints. Since all the side lengths and slope are equal, a rigid transformation like a rotation would preserve the side lengths and midpoint of each line. It also proves rotational symmetry and the only 4 figure quadralaterial that has a 90,180,270, and/or 360 degrees rotational symmetry is a square.