Answer:
B
Explanation:
Let c represent the amount of gallons used in the city and h represent the amount of gallons used on the highway.
Graham drove a total of 200 miles. Since his car gets 25 miles per gallons in the city and 30 miles per gallon on the highway:
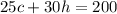
And he used a total of seven gallons. In other words:
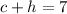
This yields a system of equations:
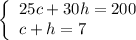
Since we want to determine the number of miles Graham drove in the city, we will solve for c using substitution. From the second equation, solve for h:
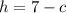
Substitute:
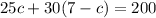
Solve for c:
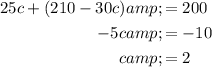
Therefore, Graham used a total of two gallons in the city.
Since his car gets 25 miles per gallon in the city, Graham drove a total of:
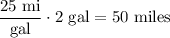
Or 50 miles in the city.
In conclusion, our answer is B.