Answer:

Explanation:
For a height h, a perimeter P, and an area A, use the following formula:
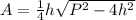
Next, replace the variables with the given values:
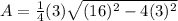
Solve the inside of the square root:

Multiply outside of the square root:

Simplify the square root:
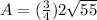
Multiply outside of the square root once more:
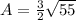
Simplify:
 , or ≈ 11.12429773
, or ≈ 11.12429773