-3x + 6y = 18 -3x = 6y+14 a) What is the slope of the 1st equation? b) What is the slope of the 2nd equation? c) Are they parallel, perpendicular, or neither?

Question

asked Oct 13, 2022 45.2k views

2 Answers

Evelie · Answer 1 · 2022-10-13T13:23:23+0000

Explanation:

-3x + 6y = 18

-3x = 6y+14

a) the slope of the 1st equation = -(-3)/6 = ½

b) the slope of the 1st equation = -3/6 = -½

c) they are niether parallel nor perpendicular

ColemanTO · Answer 2 · 2022-10-18T14:51:30+0000

Answer:

a) ¹/₂

b) -¹/₂

c) neither

Explanation:

Slope-intercept form of a linear equation:

y=mx+b

where:

Given equations:

$\begin{cases}-3x+6y=18\\-3x=6y+14 \end{cases}$

To find the slopes of the given equations, rearrange them to make y the subject then compare with the slope-intercept formula:

Equation 1

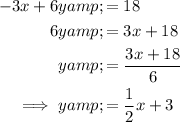
$\begin{aligned}-3x+6y & = 18\\6y & = 3x + 18\\y & = (3x+18)/(6)\\\implies y & = (1)/(2)x+3\end{aligned}$

Therefore, the slope of Equation 1 is ¹/₂.

Equation 2

$\begin{aligned}-3x & = 6y+14\\6y & = -3x-14\\y & = (-3x-14)/(6)\\\implies y& = -(1)/(2)x-(14)/(6)\end{aligned}$

Therefore, the slope of Equation 2 is -¹/₂.

Parallel slopes have the same slope.

Perpendicular slopes are at right angles to each other and therefore the product of their slopes is -1 (negative reciprocals of each other).

Therefore, the slopes of Equation 1 and Equation 2 are neither parallel or perpendicular.