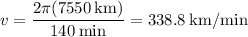Explanation:
The radius of the orbit is r = 1150 km + 6400 km = 7550 km or
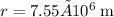
and it takes 140 minutes to complete 1 revolution. This is the same aa
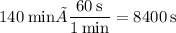
The linear speed of the satellite then is simply equal to the orbital circumference divided by the orbital period T or
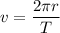
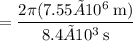
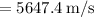
In km/min, this is