9514 1404 393
Answer:
n^2 +n +4
Explanation:
Since the divisor has only one term, the quotient is formed by dividing the terms one at a time.
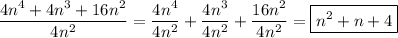
__
Your long division tableau will subtract n^2×4n^2 = 4n^4 to form the new dividend 4n^3+16n^2. Then you will subtract n×4n^2 = 4n^3 to get the new dividend of 16n^2. The final quotient term is 4, and you will subtract 4×4n^2 to get a remainder of 0. You will have written the quotient as n^2+n+4.