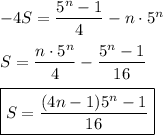Question

Find the sum Sn below:


`\displaystyle \large{S =1 \cdot 1 + 2 \cdot 5 + 3 \cdot {5}^(2) + 4 \cdot {5}^(3) + ... + n \cdot {5}^(n - 1) }`
Please show your work too. Thanks!​

Answer 1

The sum S can also be expressed as

`S = \displaystyle \sum_(k=1)^n k\cdot5^(k-1)`

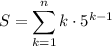
As a first step, pull out a factor of 5 from the sum:

`S = \displaystyle 5 \sum_(k=1)^n k\cdot 5^(k-2)`

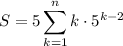
Shift the index to force the sum to start at k = 0, then distribute the summation:

`S = \displaystyle 5 \sum_(k=0)^(n-1) (k+1) 5^(k-1) \\\\ S = 5\sum_(k=0)^(n-1)k\cdot5^(k-1) + 5\sum_(k=0)^(n-1)5^(k-1) \\\\ S = 5\sum_(k=0)^(n-1)k\cdot5^(k-1) + \sum_(k=0)^(n-1)5^k`

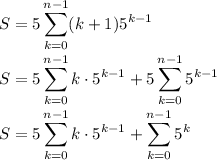
The second sum is geometric, with

`\displaystyle \sum_(k=0)^(n-1) 5^k = 1 + 5 + 5^2 + \cdots + 5^(n-1) \\\\ \implies 5\sum_(k=0)^(n-1) 5^k = 5 + 5^2 + 5^3 + \cdots + 5^n \\\\ \implies \sum_(k=0)^(n-1) 5^k - 5\sum_(k=0)^(n-1) 5^k = 1 - 5^n \\\\ \implies \sum_(k=0)^(n-1) 5^k = \frac{5^n-1}4`

This leaves us with

`\displaystyle S = 5\sum_(k=0)^(n-1)k\cdot5^(k-1) + \frac{5^n-1}4`

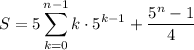
For the remaining sum, add and subtract the k = n-th term, so that we have

`\displaystyle S = 5\left(\sum_(k=0)^n k\cdot 5^(k-1) - n\cdot5^(n-1)\right) + \frac{5^n-1}4`

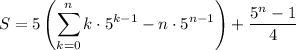
Then in the sum, we get 0 for the k = 0 term and end up recovering another copy of S :

`\displaystyle S = 5\left(S - n\cdot5^(n-1)\right) + \frac{5^n-1}4 \\\\ S = 5S - n\cdot5^n + \frac{5^n-1}4`

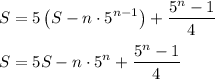
Solving for S gives

`-4S = \frac{5^n-1}4 - n\cdot5^n \\\\ S = \frac{n\cdot5^n}4 - (5^n-1)/(16) \\\\ \boxed{S = ((4n-1)5^n-1)/(16)}`