
Given :-
- We have given one function f(x) = -45x + 270
- The given function represents the total distance in miles.
- The initial interval was x = 1 and final interval was x = 3
To Find :-
- We have to find the rate of change over the given interval
Let's Begin :-
Here, We have
- Function = f(x) = -45x + 270
The given function represents the total distance in miles covered by the traveller.
Therefore,
For initial interval that is x = 1 , Distance covered by the traveller
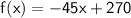
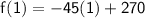
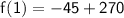
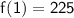
For final interval that is x = 3, Distance covered by the traveller
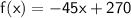
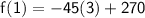
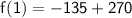
Now,
We have to find the average rate of change over the given time interval
Therefore,
Average rate of change in the given time interval
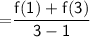
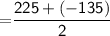

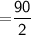
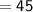
Hence, The average rate of change over the given interval is 45 miles per hour.