Question

Find the standard form of the equation of the circle with endpoints of a diameter at the points (3,4) and (-9,6).

Answer 1

• (x + 3)² + (y - 5)² = 37

Explanation:

The center is the midpoint of the diameter, the coordinates are:

• x(M) = (3 - 9)/2 = -3
• y(M) = (4 + 6)/2 = 5

The length of the diameter:

• 
  `d = √((-9-3)^2+(6-4)^2) = √(12^2+2^2) = √(148) = 2√(37)`

The radius is:

• r = d/2 =
  `2√(37) /2 = √(37)`

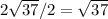
The standard form is:

• (x - h)² + (y - k)² = r², where (h, k) is the center

Substitute to get:

• (x - (-3))² + (y - 5)² = (√37)²
• (x + 3)² + (y - 5)² = 37