Answer:
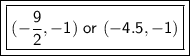
Explanation:
We are asked to find the midpoint of a line segment. When you find the midpoint, you essentially find the average of the x-coordinates and the y-coordinates. The midpoint formula is:
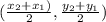
In this formula, (x₁, y₁) and (x₂, y₂) are the endpoints of the line segment. we are given the endpoints R (-6, 1) and S (-3, -3). If we match the value and the corresponding variable we see that:
- x₁= -6
- y₁= 1
- x₂= -3
- y₂= -3
Substitute the values into the formula.
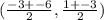
Solve the numerators.
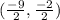
Divide.
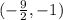
The fraction can also be written as a decimal.
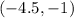
The midpoint of the line segment RS is (-9/2, -1) or (-4.5, -1).