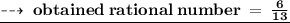Answer:
- Original Rational number is = 6/13
Explanation:
Let Numerator be : x
Denominator be : x + 7
Now,
- Numerator is increased by 6
- Denominator is decreased by 5
- the new rational number obtained is 3/2
Numerator = x + 6
Denominator = ( x + 7) - 5
According to the question,
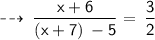

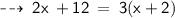
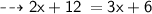
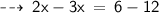
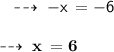
Numerator = 6
Denominator = x + 7
= 6 + 7
= 13
Thus ,