Question

Find the volume of the solid generated by revolving the region about the

A.)-axis (use washer method)
B.)-axis (use cylindrical shell method)

Answer 1

Explanation:

The region R is bounded below by y=1 and above by f(x) where

`f(x)=\begin{cases}3,&1\leq x\leq 2\\\\-x+5,&2\leq 3\end{cases}`

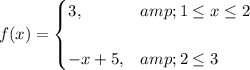
and we integrate the R over the interval [1,3]

A.

`V=\int_1^3 \pi(f(x)^2-1^2)\, dx\\V=\int_1^2 \pi(3^2-1^2)\, dx +\int_2^3 \pi((-x+5)^2-1^2)\, dx\\=9\pi + \int_2^3 \pi(x^2-10x+24)\, dx\\=9\pi +\pi\left({[(1/3)x^3-5x^2+24x]_2^3\right)\\=9\pi + \pi( (19/3) -25 +24)\\=9\pi +(16/3)\pi=43/3 \pi.`

For part B

`V=\int_1^3 2\pi x(f(x)-1)\, dx`

and you can compute the integral similarly as above, just split the integral into two integrals, one over [1,2] and the other is over [2,3].