If z^1/2 = x^1/2 + y^1/2 , prove that (x + y - z)^2 = 4xy. HELPP MEEEEE

Question

asked Jul 15, 2022 42.4k views

1 Answer

Mfjones · Answer 1 · 2022-07-20T09:07:32+0000

Answer:

Make use of the fact that
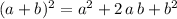$(a + b)^(2) = a^(2) + 2\, a\, b + b^(2)$ .

Explanation:

Start from the given:
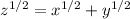z^(1/2) = x^(1/2) + y^(1/2) .

In other words:
√(z) = √(x) + √(y) .

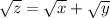Square both sides of the equation:

(√(z))^(2) = (√(x) + √(y))^(2) .

Equality would still hold because:

$\begin{aligned}& a = b \\ \implies \; & a\cdot a = a\cdot b \\ \implies \; & a \cdot a = b \cdot b \\ \implies \; & a^(2) = b^(2)\end{aligned}$ .

Simplify:

$z = (√(x))^(2) + 2\, (√(x)) \cdot (√(y)) + (√(y))^(2)$ .

z = x + 2√(x y) + y .

Subtract
from both sides of this equation:

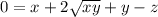0 = x + 2 √(x y) + y - z .

Subtract
2 √(x y) from both sides of this equation:

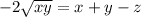-2 √(x y) = x + y - z .

Again, square both sides of this equation:

(-2 √(x y))^(2) = (x + y - z)^(2) .

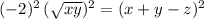$(-2)^(2)\, (√(x y))^(2) = (x + y - z)^(2)$ .

$(x + y - z)^(2) = 4\, x \, y$ (by the symmetric property of equalities.)