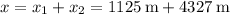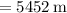Question

URGENT!!!!!!!

PLEASE HELP WITH THIS PHYSICS PROBLEM

Answer 1

Step-by-step explanation:

Let

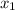`x_1` = distance traveled while accelerating

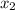`x_2` = distance traveled while decelerating

The distance traveled while accelerating is given by

`x_1 = v_0t + (1)/(2)at^2 = (1)/(2)at^2`

`\:\:\:\:\:= (1)/(2)(2.5\:\text{m/s}^2)(30\:\text{s})^2`

`\:\:\:\:\:= 1125\:\text{m}`

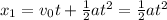
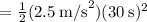
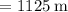
We need the velocity of the rocket after 30 seconds and we can calculate it as follows:

`v = at = (2.5\:\text{m/s}^2)(30\:\text{s}) = 75\:\text{m/s}`

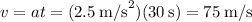
This will be the initial velocity when start calculating for the distance it traveled while decelerating.

`v^2 = v_0^2 + 2ax_2`

`0 = (75\:\text{m/s})^2 + 2(-0.65\:\text{m/s}^2)x_2`

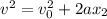
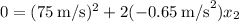
Solving for
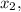`x_2,` we get

`x_2 = \frac{(75\:\text{m/s})^2}{2(0.65\:\text{m/s}^2)}`

`\:\:\:\:\:= 4327\:\text{m}`

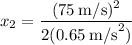
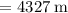
Therefore, the total distance x is

`x = x_1 + x_2 = 1125\:\text{m} + 4327\:\text{m}`

`\:\:\:\:= 5452\:\text{m}`