Question

Solve the simultaneous equations. 15 Points with explanation ❤️

Answer 1

x is equal to 2 or -5

y is equal to 1 or 8

Explanation:

first put your first equation in a format of y = x + _

here it will be :

`y = - * + 3`

now go and substitute this in your second equation. just like the picture. the pictures explain further

Answer 2

Hello there!

We are given the simultaneous equations:

`\displaystyle \large{ \begin{cases} x + y = 3 \\ {x}^(2) - 3y = 1 \end{cases}}`

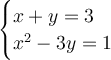
There are many methods to solve the equation but the best way for this problem is Substitution Method.

First, we have to isolate one-degree variable. I will choose the first equation to isolate. We are going to isolate y-variable so we can substitute the first equation in the second.

`\displaystyle \large{ \begin{cases} x + y = 3 \\ {x}^(2) - 3y = 1 \end{cases}}`

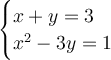
Subtract x both sides for first equation.

`\displaystyle \large{ \begin{cases} x - x+ y = 3 - x \\ {x}^(2) - 3y = 1 \end{cases}} \\ \displaystyle \large{ \begin{cases} y = 3 - x \\ {x}^(2) - 3y = 1 \end{cases}}`

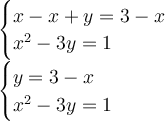
After isolating y-term, we can finally substitute y = 3-x in the second equation.

`\displaystyle \large{ \begin{cases} y = 3 - x \\ {x}^(2) - 3(3 - x) = 1 \end{cases}}`

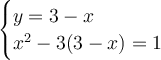
Expand -3 in. Recall that negative × negative = positive and negative × positive = negative.

`\displaystyle \large{ \begin{cases} y = 3 - x \\ {x}^(2) -9 + 3x= 1 \end{cases}}`

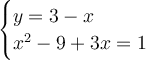
Notice that the second equation is in quadratic pattern. We are going to convert in the standard form to solve the equation.

Subtract both sides by 1.

`\displaystyle \large{ \begin{cases} y = 3 - x \\ {x}^(2) -9 - 1 + 3x= 1 - 1 \end{cases}} \\ \displaystyle \large{ \begin{cases} y = 3 - x \\ {x}^(2) -10 + 3x= 0 \end{cases}}`

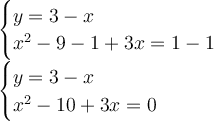
Arrange the expression in ax^2+bx+c = 0.

`\displaystyle \large{ \begin{cases} y = 3 - x \\ {x}^(2) -9 - 1 + 3x= 1 - 1 \end{cases}} \\ \displaystyle \large{ \begin{cases} y = 3 - x \\ {x}^(2) + 3x - 10= 0 \end{cases}}`

Factor the expression.

What two numbers add or subtract each others and equal to 3? (These numbers must not multiply each others and be greater than 10)

• 1+2
• 5-2
• 4-1
• 2+1

What two numbers multiply each others and equal to -10?

Check the number above and multiply two numbers.

• 1×2 = 2
• 5×(-2) = -10
• 4×(-1) = -4
• 2×1 = 2

Two numbers would be 5 and -2. Factor the expression in two brackets.

`\displaystyle \large{(x + 5)(x - 2) = 0}`

Then we solve like a linear equation, isolate both x.

`\displaystyle \large{x= - 5,2}`

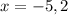
We've got two x-values. But we are not done yet.

We are going to use these values to substitute in the simultaneous equation. You can substitute in any equations; the first or second. I will choose to substitute x = -5 or x = 2 in the first equation since it is faster.

`\displaystyle \large{ \begin{cases} y= 3 - x \\ {x}^(2) - 3y = 1 \end{cases}}`

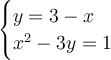
Substitute x = -5

`\displaystyle \large{ \begin{cases} y= 3 - ( - 5)\\ {x}^(2) - 3y = 1 \end{cases}} \\ \displaystyle \large{ \begin{cases} y= 3 + 5\\ {x}^(2) - 3y = 1 \end{cases}} \\ \displaystyle \large{ \begin{cases} y= 3 - ( - 5)\\ {x}^(2) - 3y = 1 \end{cases}} \\ \displaystyle \large{ \begin{cases} y= 8\\ {x}^(2) - 3y = 1 \end{cases}}`

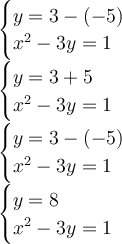
When we substitute x = -5, y = 8.

Next, substitute x = 2

`\displaystyle \large{ \begin{cases} y= 3 -2\\ {x}^(2) - 3y = 1 \end{cases}} \\ \displaystyle \large{ \begin{cases} y= 1\\ {x}^(2) - 3y = 1 \end{cases}}`

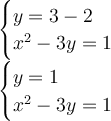
When we substitute x = 2, y = 1.

Therefore,

• x = -5, y = 8
• x = 2, y = 1

OR

• (-5,8) , (2,1) —> Coordinate Point form

Let me know if you have any questions!

Topic: Simultaenous Equations