Question

Pls need help solving this.

Answer 1

Explanation:

Given: ABC is equilateral triangle.

AD = DB & BE = EC & CF = FA ------------(IV)

Proof:

D & F are midpoint of the sides AB and AC

DF =
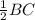`(1)/(2)BC` {Midpoint theorem}

DF = BE ----------------(I)

D & E are midpoint of the sides AB and BC

DE =
`(1)/(2)AC` {Midpoint theorem}

DE = FA ----------------(II)

E & F are midpoint of the sides BC and AC

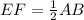`EF = (1)/(2)AB` {Midpoint theorem}

EF = AD ---------------(III)

From (I) ; (II) ; (III) ; (IV) ,

DF = DE = EF

DEF is an equilateral triangle.