Answer:
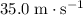 .
.
Step-by-step explanation:
The question states that the rocket gains speed steadily. In other words, the acceleration of this rocket in that four seconds would be constant.
- Let
 denote the acceleration of this rocket.
denote the acceleration of this rocket. - Let
 denote the duration of the acceleration.
denote the duration of the acceleration. - Let
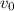 denote the initial velocity of this rocket.
denote the initial velocity of this rocket. - Let
 denote the displacement of this rocket.
denote the displacement of this rocket.
Using information from the question:
 ,
,
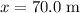 ,
,
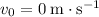 since the rocket was "initially at rest".
since the rocket was "initially at rest".
Apply the SUVAT equation
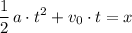 to find
to find
 , the acceleration of this rocket.
, the acceleration of this rocket.
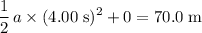 .
.
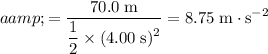 .
.
In other words, this rocket accelerated from rest at a constant
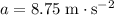 for
for
 . The final velocity of this rocket would be:
. The final velocity of this rocket would be:
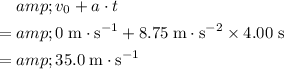 .
.