Question

The number of
`x` satisfying
`| x - 2 |^(10x^2 - 1) = |x - 2|^(3x)` is

A. 5
B. 6
C. 2
D. 4

Answer 1

D. 4

Explanation:

Without actually solving the equation, recall that for
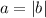`a=|b|`, there are two cases:

`\begin{cases}a=b, \\a=-b\end{cases}`

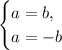
In the given equation
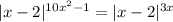`|x-2|^(10x^2-1)=|x-2|^(3x)`, there are two pairs of absolute value symbols.

Since each has two cases, there must be a total of
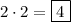`2\cdot 2=\boxed{4}` different equations created.

All four cases are:

`\begin{cases}(x-2)^(10x^2-1)=(x-2)^(3x),\\(-x+2)^(10x^2-1)=(x-2)^(3x),\\(x-2)^(10x^2-1)=(-x+2)^(3x),\\(-x+2)^(10x^2-1)=(-x+2)^(3x)\end{cases}`

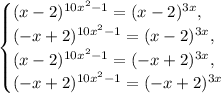
Exponents differ, hence clearly there are four possible solutions to this equation.

You can solve for all four values of
`x` by taking the log of both sides and using a bit of algebra to verify you have four solutions.