Question

A) Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis.

xy = 2, x = 0, y = 2, y = 4
b) Use the method of cylindrical shells to find the volume V generated by rotating the region bounded by the given curves about the specified axis.
y = x3, y = 8, x = 0; about x = 9

Answer 1

(a) See the attached sketch. Each shell will have a radius y chosen from the interval [2, 4], a height of x = 2/y, and thickness ∆y. For infinitely many shells, we have ∆y converging to 0, and each super-thin shell contributes an infinitesimal volume of

2π (radius)² (height) = 4πy

Then the volume of the solid is obtained by integrating over [2, 4]:

`\displaystyle 4\pi \int_2^4 y\,\mathrm dy = 2\pi y^2\bigg|_(y=2)^(y=4) = 2\pi (4^2-2^2) = \boxed{24\pi}`

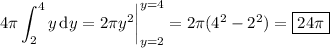
(b) See the other attached sketch. (The text is a bit cluttered, but hopefully you'll understand what is drawn.) Each shell has a radius 9 - x (this is the distance between a given x value in the orange shaded region to the axis of revolution) and a height of 8 - x ³ (and this is the distance between the line y = 8 and the curve y = x ³). Then each shell has a volume of

2π (9 - x)² (8 - x ³) = 2π (648 - 144x + 8x ² - 81x ³ + 18x ⁴ - x ⁵)

so that the overall volume of the solid would be

`\displaystyle 2\pi \int_0^2 (648-144x+8x^2-81x^3+18x^4-x^5)\,\mathrm dx = \boxed{(24296\pi)/(15)}`

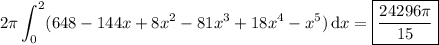
I leave the details of integrating to you.