Hello there!
We are given the equation:
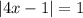
Definition/Property
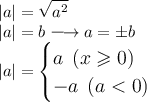
First, cancel the absolute value sign and write plus-minus beside 1.
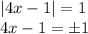
Break in two cases.
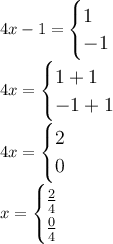
Therefore, x = 0 or 1/2
Let me know if you have any questions!
Topic: Absolute Value Function - Equations