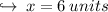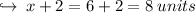Solution :
Let's solve by using Pythagoras theorem,
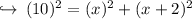
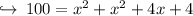
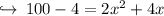
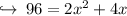
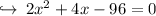
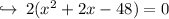
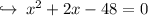
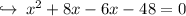
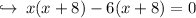
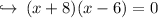
now there are two cases
Case 1 : when (x + 8) = 0
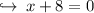
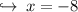
but the value of x can't be negative, since side of a triangle isn't a negative value .
Case 2 : when (x - 6) = 0

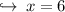
therefore the measure of other two sides are :